 |
| OwenDuffy.net |
|
The Double Bazooka Dipole is a half wave dipole with an attempt at compensation of the reactance change that occurs around resonance for a half wave dipole.
 |
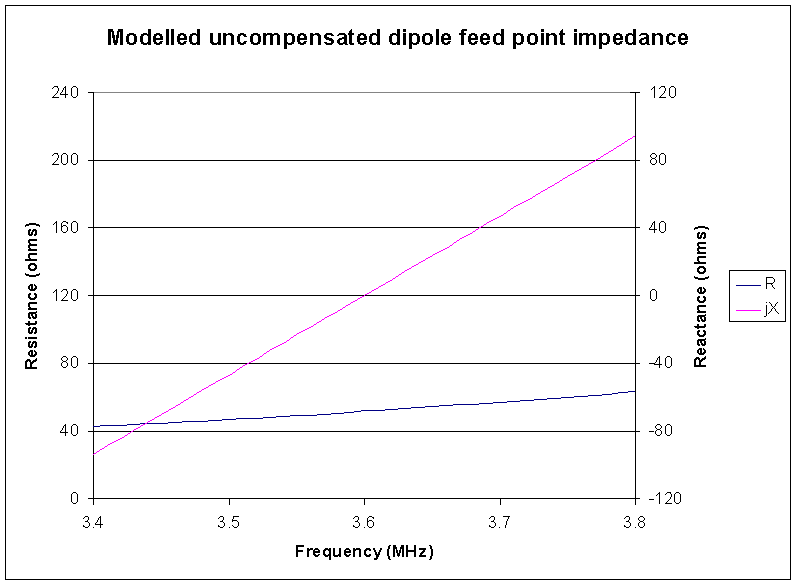
The resistance component of the feed point impedance changes slowly with frequency around resonance, and the reactance changes more quickly and is the main contribution to increase in VSWR away from resonance. Fig 1shows the change in modelled feed point impedance for a nominal half wave dipole constructed of 3.34mm diameter round copper conductor at a height of 10m above average ground.
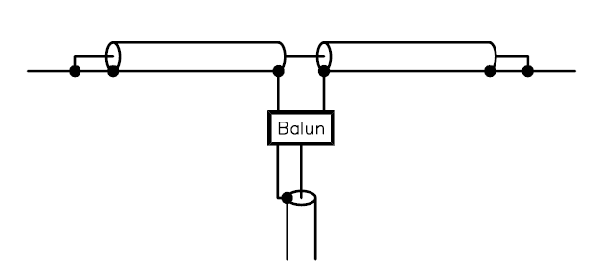 |
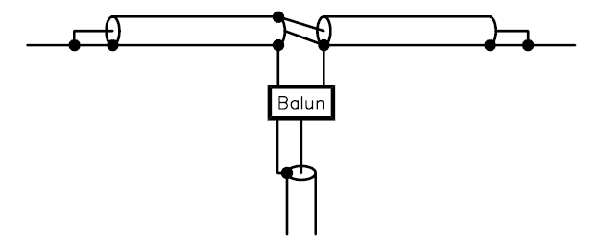
The Double Bazooka is a variation where a pair of s/c quarter wave stubs are connected in series with each other, and in shunt with the feed point. The mechanical arrangement is shown in Fig 2 (Straw, 2003).
Components of an antenna system interact with each other in a complex way, and it is important to analyse the entire antenna system (radiator, earth, transmission line, balun, ATU etc) to obtain a correct understanding of how the system works overall.
The model used for this article is a typical configuration, it uses Belden 8262 (RG58C/U) for the coax stubs, a 25m long feed line, and the legs of the dipole outboard of the stubs, and assumes an ideal balun. The model ignores the effect of the plastic jacket on the coax used for the radiator and stubs, and assumes the RF resistance of the shield is the same as a copper conductor of the same diameter. The model does not use an ATU as the load impedance is suitable for direct connection to a transmitter requiring a nominal 50Ω load.
The feed point impedance is calculated using NEC-2, the model is available here. The complex impedance of the stub is calculated using the technique used and described in the Transmission Line Loss Calculator. The feed line loss is calculated from the impedance of the feed point in shunt with the stub using the technique used and described in the Transmission Line Loss Calculator.
The calculated results and interpretations apply only to the modelled scenario.
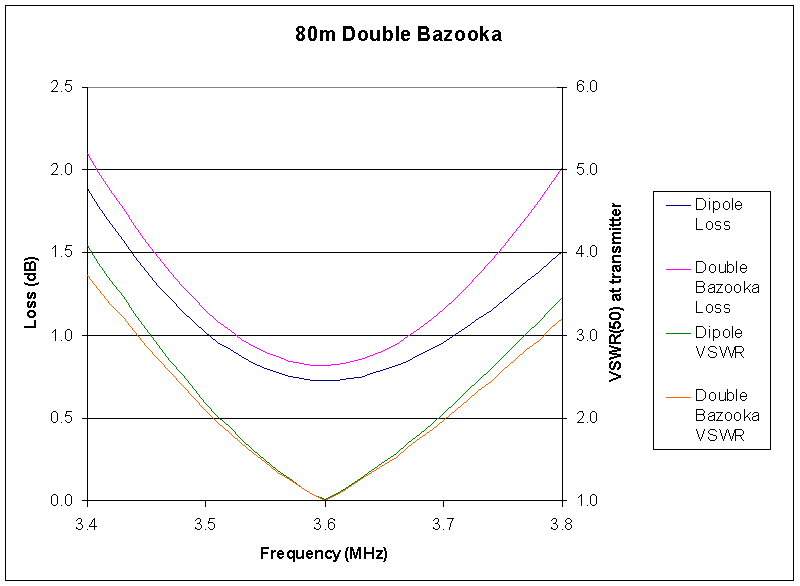 |
Fig 3 is a plot of system loss (radiator, stubs and feedline), and VSWR at the transmitter for this uncompensated dipole and this Double Bazooka.
Fig 3 shows clearly that this Double Bazooka has wider bandwidth than the equivalent uncompensated dipole, but the increase is small (15kHz or 7.5% at VSWR=2), and comes at a cost of 0.1dB to 0.5dB extra loss (up to 10% additional power loss). The difference in performance would probably deny measurement in a typical ham installation.
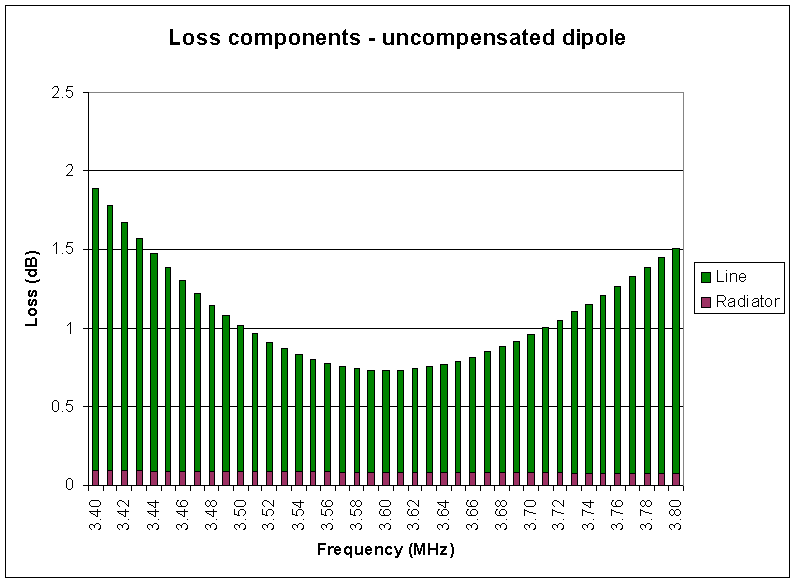 |
Fig 4 shows the system loss components of this uncompensated dipole. The line loss grows away from resonance due to the increasing VSWR.
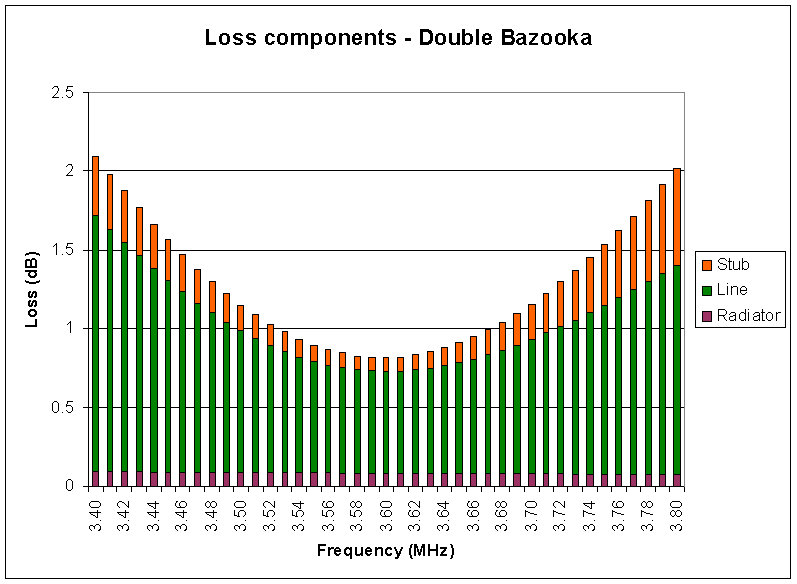 |
The Double Bazooka design is an attempt to compensate the off resonance reactance at the feed point to reduce VSWR away from resonance, and therefore to reduce line losses off resonance. Fig 5 shows the system loss components of this Double Bazooka. Note the additional loss component for the stubs, and that although the line loss component is slightly lower than in the uncompensated case, it is not sufficiently lower to offset the significant stub loss. Note that many published analyses of the Double Bazooka ignore the stub loss and so are incomplete and unreliable. Fig 4 and Fig 5 highlight the need for a system view.
The fundamental failure in the design in this case is that stubs of practical Zo do not deliver nearly enough reactance change to compensate the dipole, the stubs are in series with each other, and they add parallel compensation which drives the equivalent feed point series resistance up rather than just offsetting the reactance. It is possible that in another scenario (eg with high line loss) that the stub loss is more than offset by a reduction in line loss, but it is arguable that such a configuration is not ideal. Equally, use of a lower loss transmission line would render the Double Bazooka even less attractive.
Whilst this Double Bazooka has marginally higher bandwidth, it is at the expense of:
The Double Bazooka is a contentious antenna, mainly because of claims of magical performance. Two common claims are that:
The graphs above show that for this particular construction, the system losses for the Double Bazooka are higher than for an uncompensated dipole, ie the efficiency is lower.
The Double Bazooka is a balanced antenna, and benefits from a balun to transition to unbalanced feed line in the same way that an ordinary dipole benefits from a balun.
 |
The Cross-connected Double Bazooka (Straw, 2003) at Fig 6 is a variation where the two stubs are each connected in parallel across the feed point.
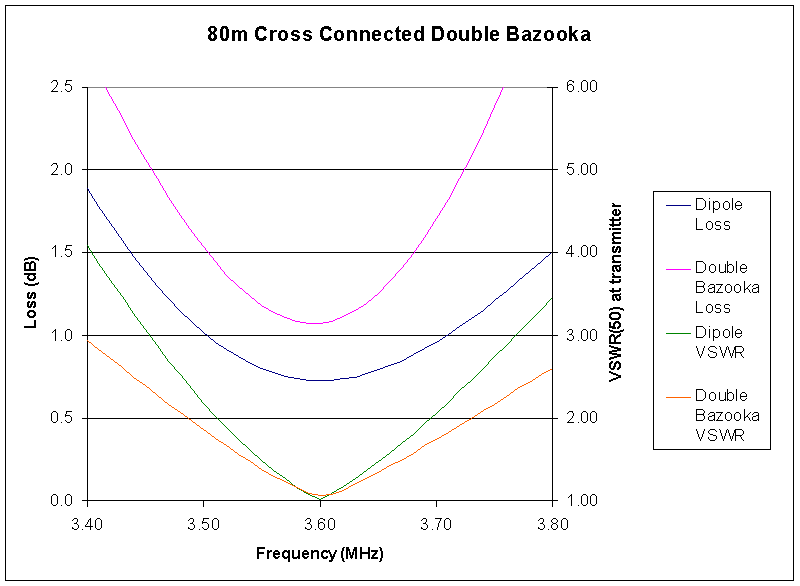 |
Fig 7 is a plot of system loss (radiator, stubs and feedline), and VSWR at the transmitter for an uncompensated dipole and the Cross-connected Double Bazooka.
The VSWR bandwidth is greater, but at the expense of even higher stub loss.
The following conclusions are made:
| Version | Date | Description |
| 1.01 | 12/05/2007 | Initial. |
| 1.02 | ||
| 1.03 |
Use at your own risk, not warranted for any purpose. Do not depend on any results without independent verification.
© Copyright: Owen Duffy 1995, 2021. All rights reserved. Disclaimer.