 |
| OwenDuffy.net |
|
A question often asked in online fora is how to adjust a short helically loaded HF vertical mobile antenna. This type of antenna is usually intended for direct coax feed, albeit at somewhat elevated VSWR. It is not uncommon that products in this part of the market do not actually specify VSWR limits.
On the low bands the feed point impedance is built out with designed in conductor loss. The helical winding uses thin wire to increase the R component of feed point Z for an 'acceptable' VSWR.
This article reports measurements of the impedance of a MobileOne M40 antenna system, a 1.8m long helically loaded whip for the 40m band to provide an example to expose some concepts.
 |
Fig 1 shows the M40 mounted on a roof rack. It has 3.2m of RG58C/U feed line.
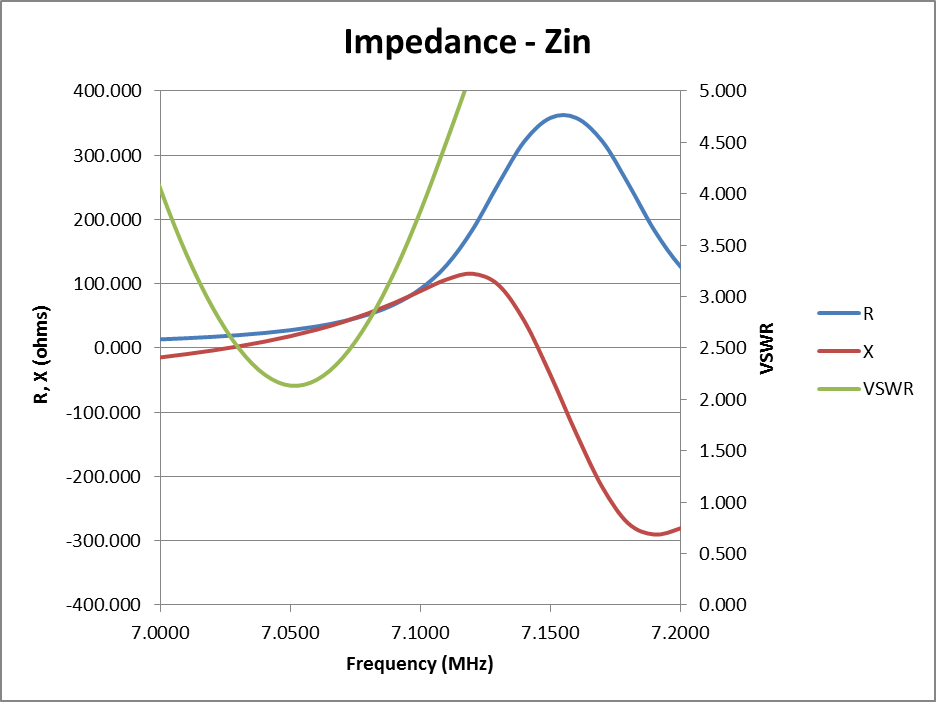 |
Fig 2 shows the impedance components R and X, and VSWR(50) (meaning VSWR wrt Zo=50+j0Ω) at the transmitter end of the feed line. These are the figures that might be read from a handheld analyser, though note that many do not display the sign of X.
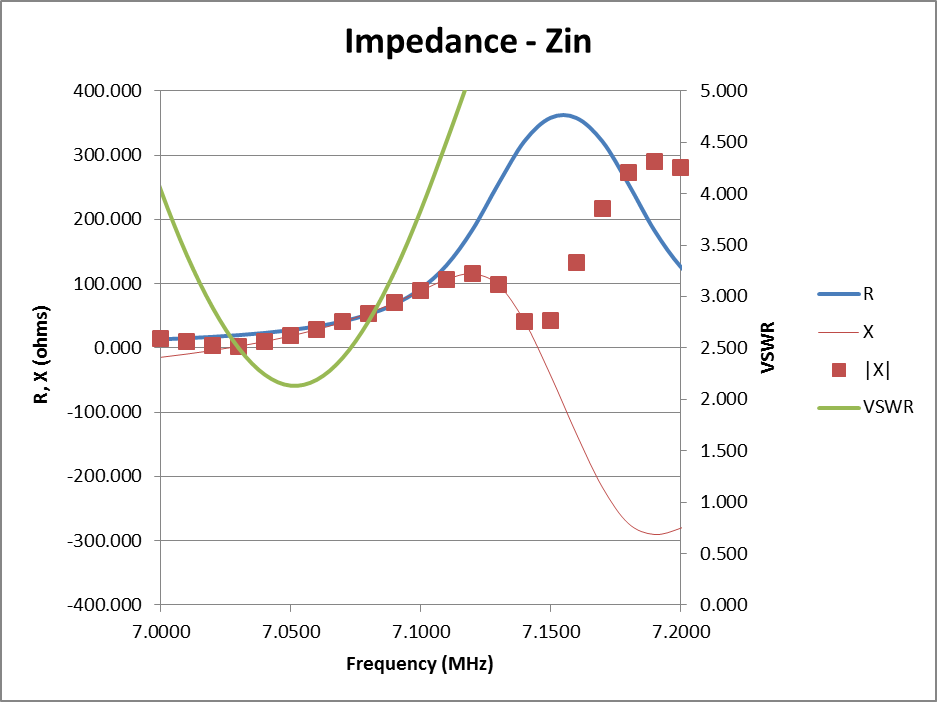 |
Fig 3 shows the impedance components R and |X|, and VSWR(50), that might be displayed by an analyser that does not show the sign of X, eg MFJ259B. The correct value of X (ie including its sign) is also shown (the feint brown line).
To complete the picture, let us look at the impedance at the base of the vertical.
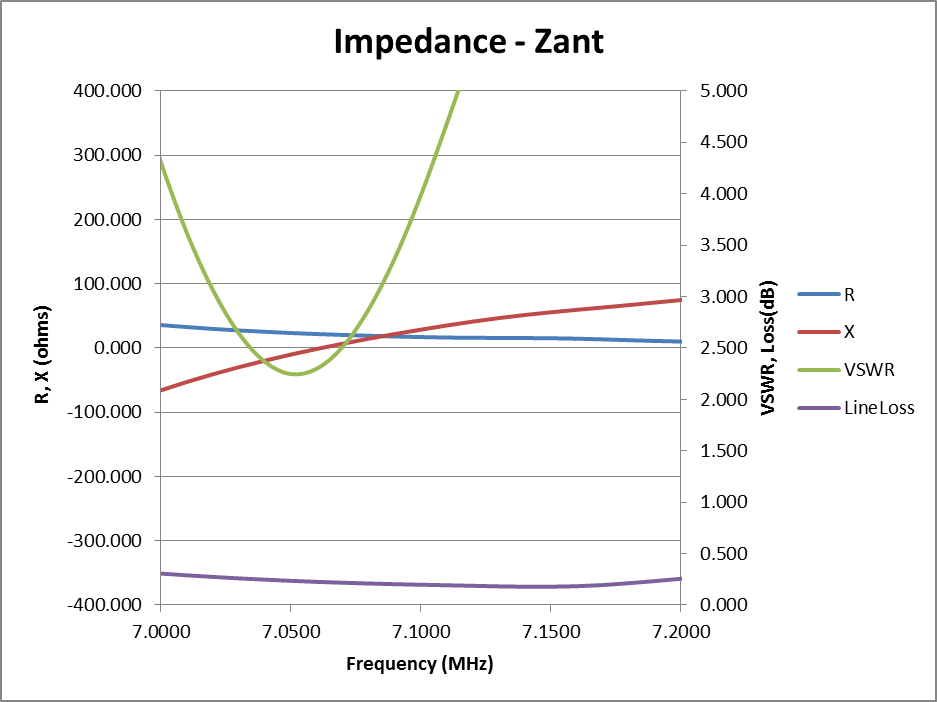 |
Fig 4 shows the impedance components R and X, VSWR(50) and line loss at the base of the antenna, calculated using the techniques used by RF Transmission Line Loss Calculator.
In all of these graphs, VSWR(50) is minimum at 7.050MHz. The vertical itself is resonant (ie X=0) at 7.060MHz, just a little above the frequency of minimum VSWR.
Fig 4 reveals how the antenna behaves. X increases for a negative value at low frequencies, fairly smoothly through resonance (X=0) to higher positive reactance at higher frequencies. The R component in this case falls smoothly from low frequencies to high frequencies.
Hams apparently have some mistaken notions about the relationship of R,X and
VSWR. For example,(WA5BEN 2012) states about this type of antenna on QRZ [i]f you
somehow mis-tune the antenna to get it to match 50 Ohms, you have added
inductive reactance or capacitive reactance to de-tune it from resonance. That
actually prevents transfer of maximum power to the antenna, because the equation
now becomes Xc (or XL) + Rr + Rg +Rc
. If we are talking of the VSWR wrt to
nominal Zo=50+j0, the lowest VSWR will always occur when X=0 for any constant
value of R. In practice, you cannot 'detune' the antenna alone to improve VSWR. His equation
reveals the cause of his misunderstanding, reactance and resistance cannot
simply be added as scalar quantities as he has done, they need to be treated as
complex quantities and if R is not equal to 50, there is no pure reactance that
can be added in series to obtain VSWR=1. The same conceptual error is demonstrated in his
continued postings:
[t]he screwdrivers that I have seen do not provide such a matching system.
They simple tune off-resonance to provide XL + Rr + Rg + Rc = ~ 50 Ohms
, and
VSWR = 1:1 when Zo of the line is matched by the impedance of the antenna --
i.e., 50 Ohm line connects to an antenna (load) of 50 Ohms. If the 50 Ohm line
is connected to a 20 Ohm antenna (pretty close to a 20 Meter 8 foot center
loaded mobile input impedance), the VSWR is 2.5:1. If a reactance of 30 Ohms is
added in series (which can be done by setting the upper antenna rod for lowest
VSWR), the transmitter / feedline will see a match, but less power will be
transferred to the antenna
.
This type of thinking is the result of not understanding that impedance is a complex quantity (having both real and imaginary parts), and the relationship between Zo, Zload and VSWR.
If the resonant feed point impedance is 20Ω, ie Z=20+j0Ω (VSWR(50)=2.5, there is no value of series reactance that will reduce VSWR(50), much less make it 1. Though WA5BEN states above that 30Ω of reactance giving Z=20+j30Ω or Z=20-j30Ω (depending on the type of reactance) will deliver VSWR(50)=1, it is actually VSWR=3.52 in both cases, worse than without his magic 30Ω of reactance!
If you cannot calculate impedance properly, then you cannot calculate VSWR on a given line.WA5BEN demonstrates that a lack of grasp of the fundamentals of complex impedance flows up into flawed interpretations of the impact on VSWR.
WA5BEN's bombastic style, hand waving that sounds quantitative but is short on specifics, squirming when he has been found out, and belittling others to promote his own position don't actually lend accuracy to content, but rather warn of content issues.
(In Fig 4, minimum VSWR is not 1:1 and it does not exactly coincide with X=0 because R is not constant, it is also changing with frequency. VSWR(50) cannot be 1:1 if X is not equal to zero. For more information on the maths of transmission lines, see Telegrapher's equation.)
This type of antenna is designed for direct coax feed without any impedance transforming networks, tuners etc. It is intended that it be adjusted in length for minimum VSWR at a frequency of interest in the relevant band.
Practical transmitters do not necessarily deliver maximum output power into a 50+j0Ω load, but they ought deliver close to their rated power into a load close to 50+j0Ω and at best linearity, so it makes sense to adjust the antenna system for close to 50+j0Ω at the transmitter, ie minimum VSWR. Minimum VSWR also delivers lowest feed line loss except for the case of very short lines where that does not necessarily apply, but the difference will usually be small.
Some folk advise tuning for resonance for best performance, and then describe a procedure to adjust the antenna length until X=0 at the frequency of interest. If this measurement is made right at the antenna base, then VSWR will also be close to minimum. If the measurement is made looking into some length of feed line, then it is unlikely that VSWR is minimum where X=0 as is demonstrated by the graphs above, nor is it likely that antenna itself is resonant.
Whilst this type of antenna is often promoted as suited for direct coax feed, the VSWR experienced may be outside the transmitter specifications and may result in reduced output from the transmitter. It will often be feasible to improve the VSWR with a suitable inductor in shunt with the feed point and retuning the vertical for a better VSWR. The inductance is specific to the antenna and band.
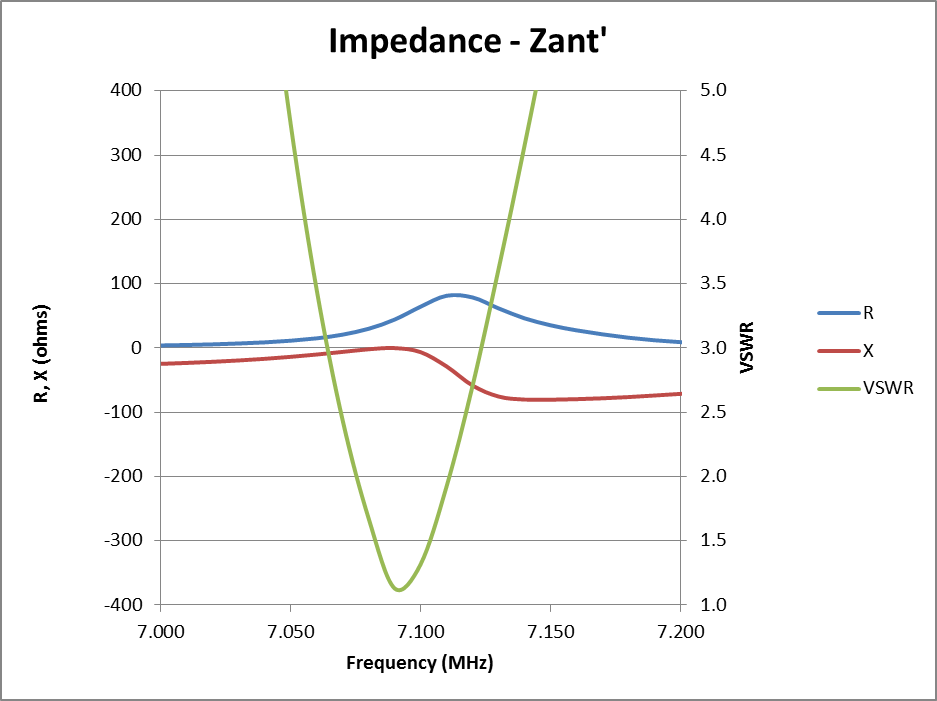 |
Fig 5 shows the impedance components R and X, VSWR(50) at the feed point of the same antenna with a shunt 0.82µH inductor (about 6 t on a 20mm form, 12mm long). VSWR is lower, although bandwidth is somewhat reduced. The centre frequency can be moved using the adjustable whip tip that is part of this antenna, and the coil adjusted for best VSWR. In this case, if the length of the whip and coil are adjusted to restore optimal VSWR at 7.050MHz, around 1µH of inductance will be required.
The benefit is that the transmitter operates into a load closer to its rated load, it will probably deliver closer to its rated power at possibly the best linearity, and line losses will be low.
If you want to know the feed point impedance, then you can measure that at the feed point. Alternatively, you can measure it at the transmitter end of the feed line and use TLLC to find the impedance at the feed point.
If you want to know the VSWR, you can measure that anywhere along the feed line, it is marginally lower at the transmitter end of the feed line as accounted for exactly by line loss. In the example above, VSWR at the antenna is 2.25 and at the transmitter it is 2.15. More importantly, the frequency where minimum VSWR occurs is the same at both ends of the line.
| Version | Date | Description |
| 1.01 | 13/01/2012 | Initial. |
| 1.02 | ||
| 1.03 |
© Copyright: Owen Duffy 1995, 2021. All rights reserved. Disclaimer.